VARIABILITE : INTER & INTRA
Il s’agit d’étudier la variabilité d’un caractère observé sur une population divisée en sous-populations ; mise en évidence de 2 sources de variabilité : INTER & INTRA ; théorème.
———-
On observe un caractère quantitatif x sur une population P de N individus.
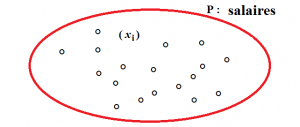
- Exemple 1 : l’ensemble P de tous les salaires \displaystyle (x_{i}) en France
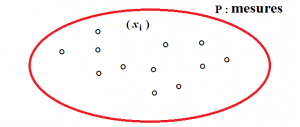
- Exemple 2 : l’ensemble P de toutes les mesures \displaystyle (x_{i}) d’une même expérience.
On suppose désormais que la population P est composée de p sous-populations \displaystyle E_{k} avec \displaystyle k\in\llbracket 1,p\rrbracket ; elles-mêmes contenant \displaystyle n_k individus.
- Exemple 1 : un salarié appartient à une branche professionnelle ; les branches professionnelles (\displaystyle E_{k}) forment une partition de l’ensemble de l’activité salariée \displaystyle (x_{ik}).
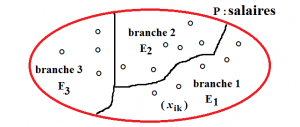
On distinguera les écarts de salaires dans les branches (intra) et entre les branches (inter).
- Exemple 2 : une mesure est réalisée par une personne ; les personnes \displaystyle E_{k} effectuant les mesures d’une même expérience forment une partition de l’ensemble des mesures de cette expérience \displaystyle (x_{ik}).
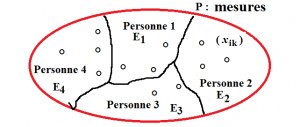
On distinguera l’erreur de mesure de répétabilité (intra) et de reproductibilité entre les personnes (inter).
- S’INFORMER (à partir d’un exemple simple numérique)
- DEMONTRER
- CONSEQUENCES