Récapitulons les notations :
| indice k → | 1 | 2 | .. k .. | p |
| sous-population Ek | E1 | E2 | .. Ek .. | Ep |
| taille nk | n1 | n2 | .. nk .. | np |
| moyenne \displaystyle \bar x_k | \displaystyle \bar x_1 | \displaystyle \bar x_2 | .. \displaystyle \bar x_k .. | \displaystyle \bar x_p |
\displaystyle x_{ik} est la valeur observée du \displaystyle i^{eme} individu de la sous-population \displaystyle E_{k} et la variance de la population est donc : \displaystyle \frac1N\sum_{i,j}{(x_{ik}-\bar{\bar x})^2}
avec
- N : le nombre d’individus de la population P : \displaystyle N=\sum_{k=1}^pn_k
- \displaystyle\overline{\overline x} : la moyenne observée sur toute la population P ; c’est aussi la « moyenne des moyennes » : \displaystyle\overline{\overline x}=\frac1N\sum_{k=1}^p{n_{k}\overline{x_k}}
————–
Pour calculer la variance de P, il faut évaluer \displaystyle \sum_{i,k}{(x_{ik}-\bar{\bar x})^2} (=SCE)
Les observations sont consignées dans un tableau à double entrée :
| les 2 indices k → i ↓ |
1 | .. k .. | p |
| 1 | : | ||
| … i … | \displaystyle x_{ik} | ||
| nk |
Débutons…
\displaystyle \sum_{i,k}{(x_{ik}-\bar{\bar x})^2}=\sum_{k=1}^p (\sum_{i=1}^{n_k}(x_{ik}-\bar{\bar x})^2) (1)
————–
La somme « double » \displaystyle \sum_{i,k} n’exigeant aucun ordre dans le « balayage » des \displaystyle x_{ik} est réorganisée en privilégiant la somme des termes de la sous-population \displaystyle E_{k} :
\displaystyle \sum_{k=1}^p (\sum_{i=1}^{n_k}…
————–
Appliquons le théorème de Pythagore dans chaque sous-population Ek:
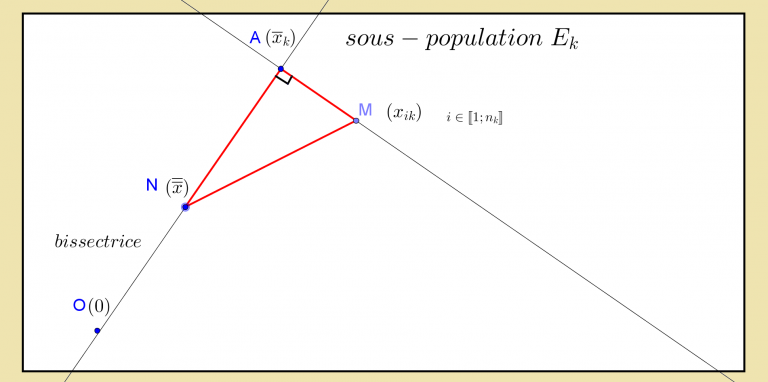
On sait que le point A est le projeté orthogonal du point M sur la bissectrice, et donc :
MN2 = MA2 + AN2
—-
Rappelons la distance euclidienne… dans un espace rapporté à un repère orthonormé…
AB²=\displaystyle (x_B-x_A)^2+(y_B-y_A)^2{+;..} avec A (\displaystyle x_A;y_A;{;..} ) et B(\displaystyle x_B;y_B;{;..}).
et qu’un point de la bissectrice a toutes ses coordonnées égales !
—-
MN2 = MA2 + AN2 avec A et N sur la bissectrice…
\displaystyle \sum_{i=1}^{n_k}(x_{ik}-\bar{\bar x})^2=\sum_{i=1}^{n_k}(x_{ik}-\bar x_k)^2+\sum_{i=1}^{n_k}(\bar x_k-\bar{\bar x})^2que l’on reporte dans l’expression initiale (1) :
\displaystyle \sum_{i,k}{(x_{ik}-\bar{\bar x})^2}=\sum_{k=1}^p \bigg(\sum_{i=1}^{n_k}(x_{ik}-\bar x_k)^2+\sum_{i=1}^{n_k}(\bar x_k-\bar{\bar x})^2\bigg) \displaystyle \sum_{i,k}{(x_{ik}-\bar{\bar x})^2}=\sum_{k=1}^p\sum_{i=1}^{n_k}(x_{ik}-\bar x_k)^2+\sum_{k=1}^p{n_k}(\bar x_k-\bar{\bar x})^2 \displaystyle \sum_{i,k}{(x_{ik}-\bar{\bar x})^2}=\sum_{i,k}(x_{ik}-\bar x_k)^2+\sum_{k=1}^p{n_k}(\bar x_k-\bar{\bar x})^2
En divisant chaque membre par l’effectif total N, apparaît :
| une relation | \displaystyle\sigma^2=\sigma_1^2+\sigma_2^2 |
| \displaystyle\sigma^2 : variance de la population | \displaystyle\sigma^2=\frac1N\sum_{i,k}{(x_{ik}-\bar{\bar x})^2} |
| \displaystyle\sigma_1^2 : variance intra-(populations) | \displaystyle\sigma_1^2=\frac1N\sum_{i,k}(x_{ik}-\bar x_k)^2 |
| \displaystyle\sigma_2^2 : variance inter-(populations) | \displaystyle \sigma_2^2=\frac1N\sum_{k=1}^p{n_k}(\bar x_k-\bar{\bar x})^2 |
| v= variance | vINTRA+vINTER = vTOTALE |
Autre version de ce même résultat.