Si SCE (a ; b ) atteint son minimum alors on montre que b doit être égal à :
b = \displaystyle\frac {1}{n}(\sum_{i=1}^n y_i)-a (\frac {1}{n}\sum_{i=1}^n x_i) Preuve A
ou encore : en utilisant « x barre » et « y barre » pour désigner les moyennes,
\displaystyle b =\bar y-a\bar x
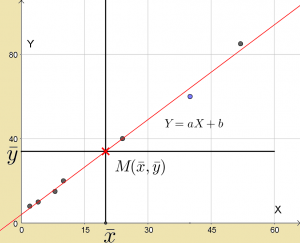
\displaystyle \bar y=a\bar x + b
| Le point moyen M (\displaystyle \bar x ; \bar y) appartient donc à la droite cherchée. |
Ce n’est pas banal ! Ci-dessous une famille de droites passant par le point moyen.
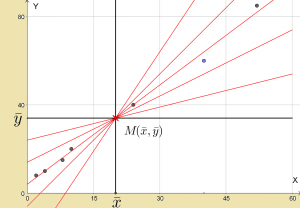
On a : \displaystyle b =\bar y-a\bar x
En reportant la valeur de b dans SCE, celle-ci atteint son minimum lorsque :
a = \displaystyle\frac {\sum_{i=1} ^n (x_i-\bar x)(y_i-\bar y)}{\sum_{i=1}^n (x_i-\bar x)^2} Preuve B
C’est le rapport entre la somme des produits des écarts et la somme des carrés des écarts de x.
Que l’on écrit : \displaystyle a=\frac{SPE_{xy}}{SCE_x}
On obtient alors une unique droite :