la loi uniforme
La loi uniforme est une loi de probabilité simple.
Celle du pur hasard.
Celle de l’équiprobabilité.
Elle n’est pas stable pour l’addition.
La simulation d’une telle loi est simple à mettre en place grâce au générateur de nombres aléatoires intégré dans les différents systèmes de calculs : calculatrice, ordinateur …
Les aléas générés sont par défaut des réels compris entre 0 et 1.
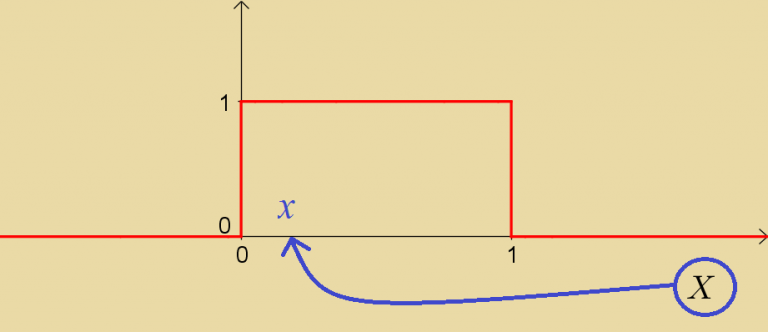
Soit X une v.a. de loi uniforme U continue à valeurs dans [0;1].
 On a:
On a:
| \displaystyle E(X)=\frac{1}{2}\quad et \quad V(X)=\frac{1}{12} |
un n-échantillon
Soit un n-échantillon aléatoire \displaystyle{\big(X_1, X_2, \;\;\ldots \;\;, X_n\big)}
Les variables aléatoires sont indépendantes et supposées suivre la même loi uniforme U.
Précisons alors l’espérance mathématique μ et la variance σ2 de la somme
\displaystyle {S}={X_{1}+X_{2}+. . .+X_{n}}
| \displaystyle \mu=\frac{n}{2}\qquad\quad \sigma^2=\frac{n}{12} |
La somme S représente « n ajouts successifs du pur hasard ». On montre que progressivement, quand n augmente, la somme S est de moins en moins « hasardeuse » et qu’elle obéit, en fin de compte, à la loi normale.
algorithme et simulation
Dans la suite, on considère les événements (E1) et (E2) :
\displaystyle (E_1)\quad{Y}\in\big[\mu-\sigma\;;\;\mu+\sigma\big]
\displaystyle (E_2)\quad{Y}\in\big[\mu-2\sigma\;;\;\mu+2\sigma\big]
de probabilités bien connues si Y est une variable aléatoire normale :
\displaystyle p(E_1)=0,6827\quad\grave{a}\;10^{-4}
\displaystyle p(E_2)=0,9545\quad\grave{a}\;10^{-4}
On se base sur l’approche fréquentiste de la probabilité.
Sur 10000 échantillons de n nombres réels compris entre 0 et 1, on recense ceux dont la somme S réalise les événements E1 et E2 [2 essais]. Ce décompte est ensuite comparé à celui obtenu par la loi normale.
Pour lancer la simulation, cliquez sur les boutons suivants :
| La taille n de l’échantillon |
Evénement | 10000 échantillons | Loi normale | ||||
| E1 |
|
6827 | |||||
| E2 |
|
9545 |
l’algorithme
[sous format Word]
Utiliser une calculatrice
[dans un cas particulier : sur 100 échantillons de n = 3 réels compris entre 0 et 1]
——-
\displaystyle{S} est la somme des 3 réels de moyenne \displaystyle \mu et d’écart type \displaystyle \sigma.
\displaystyle \mu=\frac{n}{2}=1,5\qquad\quad \sigma^2=\frac{n}{12}=0,25=0,5^2
Les événements (E1) et (E2) se mettent donc sous la forme :
\displaystyle{S}\in\big[1,5-t\times 0,5\;;\;1,5+t\times 0,5\big] où \displaystyle{t}\in\big\{1,2\big\}
Sur les 100 échantillons de 3 nombres réels compris entre 0 et 1, on recense ceux dont la somme S réalise les événements E1 ou E2. Ce décompte est ensuite comparé à celui obtenu par la loi normale.
Pour la simulation, on crée un programme sur TI. [Feuille au format Word ci-dessous]