Une méthode du dosage de l’azote total dans l’eau, est caractérisée pour des concentrations de l’ordre de 10 mg.L-1 par un écart type σ égal à 0,42 mg.L-1 .
(la loi de distribution est la loi normale)
Le ministère de l’Environnement, chargé d’accorder les agréments pour le dosage de l’azote total dans l’eau, envoie aux laboratoires demandeurs une solution étalon dont la concentration C0 est voisine de 10 mg.L-1 . Chaque laboratoire effectue 3 mesures en appliquant la méthode imposée par le ministère et renvoie la moyenne \displaystyle \overline x de ses 3 résultats.
Le ministère impose aux laboratoires un risque α de 4% de se voir refuser l’agrément alors qu’ils appliquent correctement la méthode.
la règle de décision que doit adopter le ministère
Soit μ la vraie concentration de l’azote total du prélèvement de la solution étalon analysé par le laboratoire. Le test de validation se présente donc ainsi :
| H0 : μ = C0 opposée à H1 : μ ≠ C0 |
L’hypothèse nulle H0 : μ = C0 est l’hypothèse préférentielle indiquant que le laboratoire est supposé appliquer correctement la méthode de dosage de l’azote total dans l’eau.
Soit \displaystyle \overline X la variable aléatoire associant la moyenne \displaystyle \overline x des 3 mesures :
\displaystyle \overline{X}\hookrightarrow\mathcal{N}(C_0\;;\;\frac{0,42}{\sqrt{3}})
On construit l’intervalle d’acceptation de H0 en recherchant le réel h tel que : (risque α de 4%)
| \displaystyle P\;(\overline{X} \in\big[C_0-h\;;\;C_0+h\big]){= 0.96} |
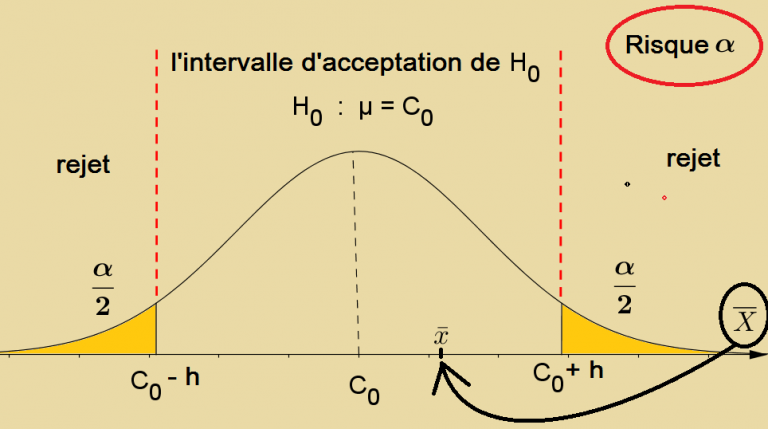A l’aide d’un logiciel, h = 0,50 mg.L-1 à 0,01.
D’où la règle de décision que doit adopter le ministère, à partir d’une moyenne \displaystyle \overline x observée par le laboratoire sur un échantillon de 3 mesures :
| si \displaystyle \overline{x} \in [C0-0,50 ; C0+0,50], H0 est acceptée, si \displaystyle \overline{x} \notin [C0-0,50 ; C0+0,50], H0 est refusée au risque α de 4%. |
et, dans le contexte :
| si \displaystyle \overline{x} \in [C0-0,50 ; C0+0,50], l’agrément est accordé, si \displaystyle \overline{x} \notin [C0-0,50 ; C0+0,50], l’agrément est refusé au risque, pour le laboratoire, de se voir refuser l’agrément alors qu’il applique correctement la méthode. (refus à tort : α = 4%) |
l’erreur systématique tolérée
Le ministère veut pouvoir refuser, avec une forte probabilité (90%) son agrément à un laboratoire qui appliquant mal la méthode de dosage, sous-estimerait (ou surestimerait) systématiquement la concentration en azote total de la solution étalon.
Il s’agit de déterminer, pour quelle erreur Δ systématique, les laboratoires se verront refuser l’agrément.
On désigne toujours par C0 la concentration « référence » de la solution étalon,
et par C1 la concentration « référence faussée » :
| Δ = C0 -C1 |
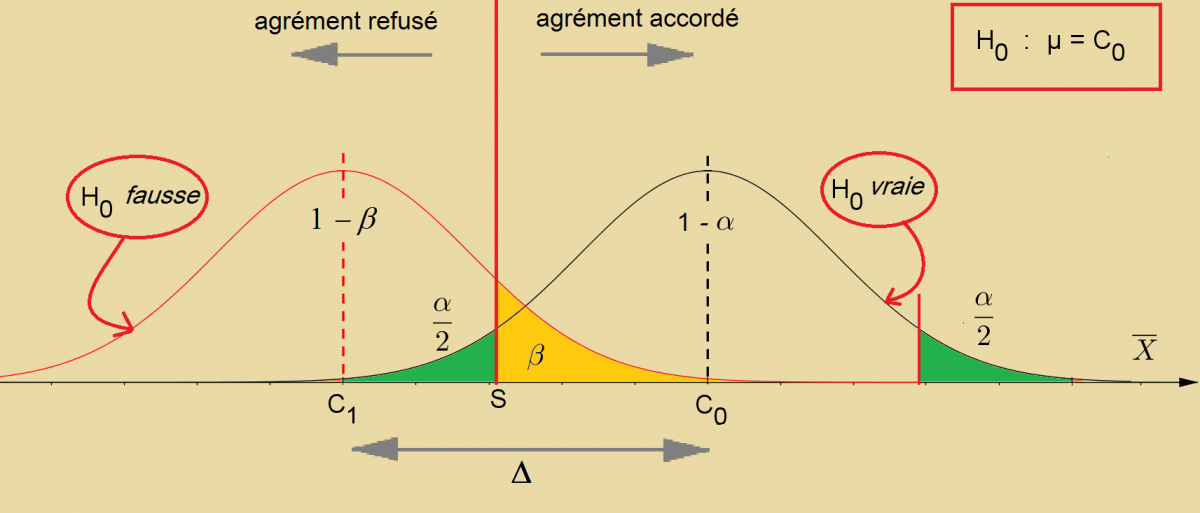
La puissance du test est la probabilité du « refus à bon escient » fixé par le ministère à 90% (= 1-β).
et β est le risque, pour le ministère, d’accorder l’agrément à un laboratoire qui applique mal la méthode.
Le calcul conduit à : \displaystyle S=C_0-t_0\times\frac{\sigma}{\sqrt{n}} et \displaystyle S=C_1+t_1\times\frac{\sigma}{\sqrt{n}}
donc,
| \displaystyle \Delta=\frac{(t_0+t_1)\times\sigma}{\sqrt{n}} | |
| n = 3 σ = 0,42 mg.L-1 | |
| 1-β = 0,9 | t1 = 1,28 |
| α = 0,04 | t0 = 2,05 |
| Δ = 0,81 mg.L-1 à 0,01. |
pour une erreur systématique tolérée de 0,50 mg.L-1
on peut calculer le nombre de mesures à effectuer par le laboratoire :
| \displaystyle n=\Big(\frac{(t_0+t_1)\times\sigma}{\Delta}\Big)^2 | |
| Δ = 0,5 mg.L-1 σ = 0,42 mg.L-1 | |
| 1-β = 0,9 | t1 = 1,28 |
| α = 0,04 | t0 = 2,05 |
| n = 8 |