On cherche à exprimer la conductivité Y en fonction des teneurs en métaux M1 et M2.
On décide alors d’essayer … en appliquant le modèle polynomial suivant : ( du « premier degré » )
Y = a0 + a1X1 + a2X2 +a12 X1X2 avec :
- a0 ; a1 ; a2 et a12 des coefficients à estimer au mieux,
- X1 la variable centrée réduite : X_1\in[-1,+1] associée au facteur F1 la teneur en métal M1.
- X2 la variable centrée réduite : X_2\in[-1,+1] associée au facteur F2 la teneur en métal M2.
Pour présenter et effectuer les calculs, on utilise la disposition suivante (selon l’ordre de l’algorithme de Yates) :
| Plan | I | X1 | X2 | X1X2 | Y |
| Essai n°1 | 1 | -1 | -1 | 1 | 134 |
| Essai n°2 | 1 | 1 | -1 | -1 | 140 |
| Essain°3 | 1 | -1 | 1 | -1 | 118 |
| Essai n°4 | 1 | 1 | 1 | 1 | 120 |
| coefficients → | a0 | a1 | a2 | a12 |
Déterminons chaque coefficient :
On a : \Bigg\lbrace \begin{array}{l}a_0-a_1-a_2+a_{12}=134\\a_0+a_1-a_2-a_{12}=140\\a_0-a_1+a_2-a_{12}=118\\a_0+a_1+a_2+a_{12}=120\end{array}
Les coefficients s’obtiennent aisément par addition membre à membre après avoir appliqué à chaque ligne du système les coefficients 1 ou (-1) de la colonne correspondante. Ne pas oublier de diviser par 4.
| \begin{array}{l} a_0=\frac{1\times 134+1\times 140+1\times 118+1\times 120}{4}=128 \\\\a_1=\frac{(-1)\times 134+1\times 140+(-1)\times 118+1\times 120}{4}=2 \\\\a_2=\frac{(-1)\times 134+(-1)\times 140+1\times 118+1\times 120}{4}=-9 \\\\a_{12}=\frac{1\times 134+(-1)\times 140(-1)\times 118+1\times 120}{4}=-1\end{array} |
On obtient donc la conductivité thermique de l’alliage en fonction des niveaux des facteurs :
Un coefficient = un effet
- Supposons que seul le premier facteur (la teneur en M1 ) agisse sur la conductivité Y, il faut annuler X2 :
X2=0 ⇒ Y = 128 + 2X1 ainsi :
au niveau bas, Y = 128 + 2(-1) = 126
au niveau haut, Y = 128 + 2(+1) = 130 soit un GAIN de 4 W de conductivité.
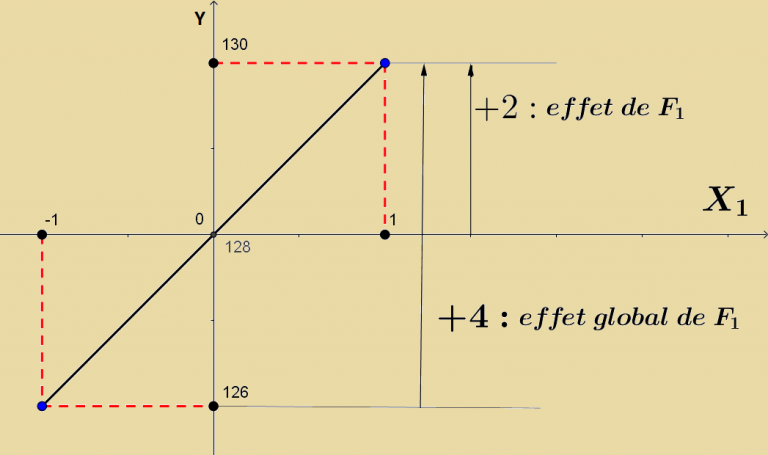
on retrouve l’effet global du premier facteur +4 ;
| Le coefficient a1 = 2 est donc l’effet du premier facteur et son double est l’effet global. |
- Supposons que seul le deuxième facteur agisse sur la conductivité Y, il faut annuler X1 :
X1=0 ⇒ Y = 128 – 9X2 ainsi :
au niveau bas, Y = 128 – 9(-1) = 137
au niveau haut, Y = 128 – 9(+1) = 119 soit un PERTE de 18 W de conductivité.
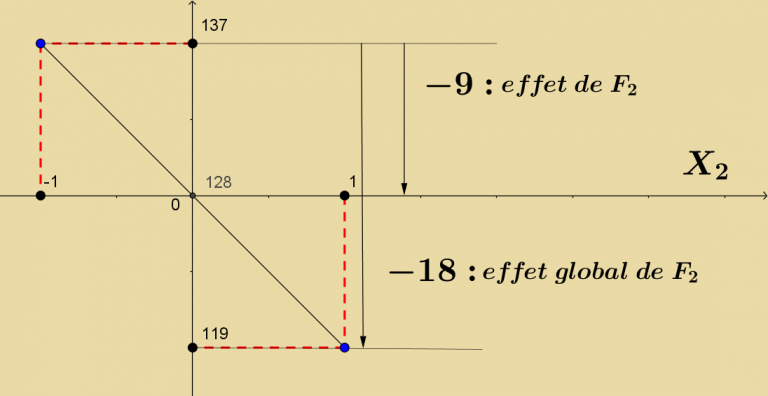
on retrouve l’effet global du premier facteur -18 ;
| Le coefficient a2 = -9 est donc l’effet du deuxième facteur et son double est l’effet global. |
- Supposons qu’aucun des deux facteurs n’agisse sur la conductivité Y, il faut annuler X1 et X2 :
X1=X2 = 0 ⇒ Y = 128 ainsi :
| Le coefficient a0 = 128 est donc l’effet du facteur « neutre » que l’on note I (application identique en algèbre). C’est également la conductivité moyenne. |
- Supposons que les deux facteurs agissent sur la conductivité Y,
| Le coefficient a12 = -1 est l’effet de l’interaction qui est vu comme un nouveau facteur : le facteur « produit » . |
vocabulaire
Les calculs sont présentés et regroupés au sein d’un tableau appelé matrice. C’est une construction. On respectera l’ordre de l’algorithme de Yates. On dit :
construire la matrice des calculs des effets
ce qui donne sur cet exemple :
| Plan complet | I | X1 | X2 | X1X2 | Y |
| Essai n°1 | 1 | -1 | -1 | 1 | 134 |
| Essai n°2 | 1 | 1 | -1 | -1 | 140 |
| Essain°3 | 1 | -1 | 1 | -1 | 118 |
| Essai n°4 | 1 | 1 | 1 | 1 | 120 |
| coefficients → | a0 | a1 | a2 | a12 | |
| effets → | 128 | 2 | -9 | -1 |