Les plans complets
- Le facteur F1 a deux niveaux : le niveau bas noté – et le niveau haut noté +
- Le facteur F2 double les combinaisons et ainsi de suite… comme l’illustre l’arbre :
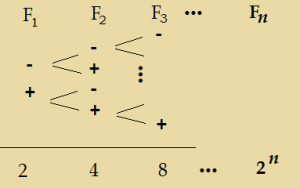
2 facteurs {F1,F2} à 2 niveaux {-,+} conduit à 4 combinaisons et donc 4 essais,
3 facteurs {F1,F2,F3} à 2 niveaux {-,+} conduit à 8 combinaisons et donc 8 essais.
Le plan est complet lorsque l’on planifie tous les essais. On parle alors de :
| plan complet 2n (n facteurs à 2 niveaux ) |
Dénombrer les effets d’un plan complet 2n
Les facteurs F1, F2, …Fn agissent sur la réponse expérimentale Y. On distingue alors les effets des facteurs et des interactions sur la réponse.
| Plans complets | Nombre d’essais | Nombre d’effets |
| 2 facteurs à 2 niveaux |
22 | 1 effet a0 du facteur neutre I ou moyenne, 2 effets a1, a2 des 2 facteurs F1, F2 1 effet a12 de l’interaction F1F2 |
| 3 facteurs à 2 niveaux |
23 | 1 effet a0 du facteur neutre I ou moyenne, 3 effets a1, a2, a3 des 3 facteurs F1, F2, F3 3 effets a12, a13, a23 des interactions 2 à 2 1 effet a123 de l’interaction entre les 3 facteurs. |
| n facteurs à 2 niveaux |
2n |
\Big( \begin{array}{l}n\\0\end{array}\Big)=1 effet a0 du facteur neutre I ou moyenne, \Big( \begin{array}{l}n\\1\end{array}\Big)=n effets a1, a2… an des n facteurs F1, F2… Fn |
On remarque que le nombre d’essais d’un plan complet est égal au nombre de tous les effets des différents facteurs et interactions :
2 facteurs 1+2+1 = 4 = 22
3 facteurs 1+3+3+1 = 8 = 23
n facteurs \displaystyle\sum_{k=0}^{n}\Big( \begin{array}{l}n\\k\end{array}\Big)=(1+1)^n=2^n
en utilisant la formule du binôme de Newton \displaystyle (a+b)^n=\sum_{k=0}^{n}\Big( \begin{array}{l}n\\k\end{array}\Big)a^kb^{n-k}
\displaystyle \Big( \begin{array}{l}n\\k\end{array}\Big) se lit « k parmi n » et sont les coefficients binomiaux :
1
11
121
1331
14641
…
conclusion
Un plan complet 2n nécessite d’effectuer 2n mesures. A partir de ces résultats, on calculera les 2n effets des facteurs et des interactions.