calculer

Procédons par étapes :

1. La droite de régression cherchée Y=a X + b obtenue par la méthode des moindres carrés passe par le point moyen :

i  →	1	2	3	4	5	6	7	∑	Moy
\displaystyle x_i	2	4	8	10	24	40	52	140	20
\displaystyle y_i	8	10	15	20	40	60	85	238	34

On obtient :

\displaystyle\bar x = 20 et \displaystyle\bar y = 34

La droite cherchée passe par le point M ( 20 ; 34)

2. Reste à obtenir le coefficient directeur a de la droite.
Rassemblons dans un tableau les différents écarts :

i  →	1	2	3	4	5	6	7	∑
\displaystyle x_i-20	-18	-16	-12	-10	4	20	32
\displaystyle y_i-34	-26	-24	-19	-14	6	26	51
\displaystyle (x_i -20)(y_i-34)	468	384	228	140	24	520	1632	3396
\displaystyle (x_i-20)^2	324	256	144	100	16	400	1024	2264

a = \displaystyle \dfrac{\sum_{i=1}^{n}(x_i-\bar x)(y_{i}-\bar y)}{\sum_{i=1}^{n}(x_i-\bar x)^2}=\frac{3396}{2264}= 1,5

Soit :   Y = a X + b

Y= 1,5 X + b

or, 34 = 1,5×20 + b  donc b = 4

ainsi :

Y = 1,5 X + 4

Les calculatrices donnent directement le résultat.

3. La qualité de l’ajustement réside dans le calcul du SCE résiduel.
On rassemble les résultats  dans un tableau :

i  →	1	2	3	4	5	6	7	∑
\displaystyle y_i	8	10	15	20	40	60	85
\displaystyle \widehat{y_i}=1,5x_i+4	7	10	16	19	40	64	82
\displaystyle (y_i-\widehat{y_i})^2	1	0	1	1	0	16	9	28

Donc : SCE (résiduel) = \displaystyle \sum_{i=1}^n(y_i-\widehat{y_i})^2 = 28

ce résultat est à comparer au SCE (total) que l’on calcule avant l’ajustement en considérant la droite « horizontale » : y = \displaystyle \bar y .

i  →	1	2	3	4	5	6	7	∑
\displaystyle y_i	8	10	15	20	40	60	85
\displaystyle \bar y	34	34	34	34	34	34	34
\displaystyle (y_i-\bar y)^2	676	576	361	196	36	676	2601	5122

Donc : SCE (Total) = \displaystyle \sum_{i=1}^n(y_i-\bar y)^2 = 5122

D’où la décomposition : Total = Expliqué + Résiduel

\displaystyle\underbrace{5122}_{total}=\underbrace{5094}_{explique}+\underbrace{28\;}_{residuel}

 

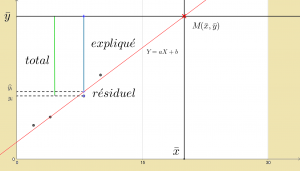
en pourcentage, cela donne :

\displaystyle 1=\underbrace{\frac{5094}{5122}}_{R^2}+\frac{28}{5122}

 

R² est le coefficient de détermination donne, en pourcentage, la « réduction » obtenue par l’ajustement tandis que 1-R² donne le « résiduel ».

R² = 99,45%      1-R² = 0,55%  (que donne la calculatrice)

Le coefficient de corrélation linéaire noté r est très utilisé en statistiques. Il « mesure » le degré de dépendance entre les 2 grandeurs X et Y. Il permet d’apprécier la qualité de l’ajustement en retournant un réel compris entre -1 et 1. ( entre -100% et +100% )

Lorsque la dépendance entre les 2 grandeurs est optimale ±100%, l’ajustement affine est parfait. Tous les points sont alignés.
Son expression est symétrique :  r = \displaystyle \frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2\sum_{i=1}^n(y_i-\bar{y})^2}}

On démontre, dans le cas d’un ajustement linéaire que : r²=R²   Preuve C