Généralités
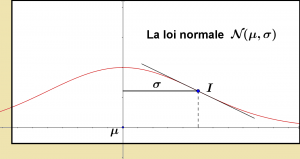
La loi normale se caractérise par une fonction analytique à 2 paramètres :
- μ qui situe l’axe de symétrie du tracé,
- σ qui donne la distance séparant cet axe de l’inflexion du tracé. (σ>0)
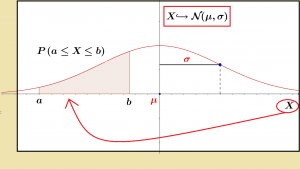
On introduit ensuite une variable aléatoire X qui suit la loi normale. Le schéma met en évidence :
- la variable X qui prend ses valeurs (une à la fois ! ) sur l’axe des abscisses,
- la probabilité que la variable X prenne une valeur entre a et b. (aire)
et se formalise ainsi : \displaystyle P\;(a\le X\le b)
E(X) est l’espérance mathématique de la variable X ; est la valeur attendue [expected value] ; est aussi la moyenne (virtuelle) des valeurs prises par X.
V(X) est la variance de la variable X.
On démontre que :
| \displaystyle E(X)=\mu | \displaystyle V(X)=\sigma^2 |
| on dit que : la variable X suit la loi normale de moyenne μ et d’écart type σ. on écrit : \displaystyle X \hookrightarrow\mathcal{N}(\mu,\sigma) |
|
Un cas particulier important
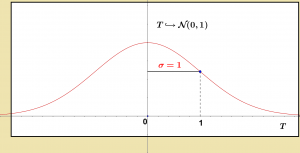
C’est la loi normale centrée réduite. Elle est centrée sur 0 (moyenne μ = 0) et son écart type est ramené à l’unité (σ = 1).
A l’aide d’une calculatrice ou un logiciel, on précise la probabilité souhaitée :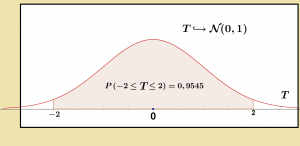
L’intérêt est que toute loi normale s’y ramène ! Et parfois c’est nécessaire.
| \displaystyle X \hookrightarrow\mathcal{N}(\mu,\sigma)\Rightarrow\frac{X-\mu}{\sigma}\hookrightarrow\mathcal{N}(0,1) |
AINSI : à \displaystyle 10^{-2} …
0,95 =\displaystyle P\;(-2\le T \le 2)
0,95 =\displaystyle P\;(-2\le \frac{X-\mu}{\sigma} \le 2)
0,95 =\displaystyle P\;(\mu-2\sigma\le X \le \mu +2\sigma)
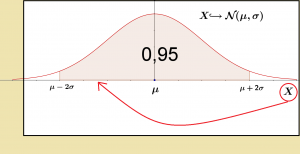
De la variable aléatoire X à l’intervalle aléatoire [X-2σ ; X+2σ]
0,95 =\displaystyle P\;(\mu-2\sigma\le X\le \mu +2\sigma)
0,95 =\displaystyle P\;(-2\sigma\le X-\mu\le +2\sigma)
0,95 =\displaystyle P\;(-2\sigma\le \mu-X \le +2\sigma)
0,95 =\displaystyle P\;(X-2\sigma\le \mu \le X+2\sigma)
ET… : cqfd
| \displaystyle P\;(\mu\in\big[X-2\sigma\;;\;X+2\sigma\big]) = 0,95 (calcul arrondi au centième) |