application numérique

Représentation visuelle

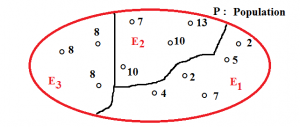
Soit une population P composée de p =3 sous-populations \displaystyle (E_{k}) avec \displaystyle k\in\llbracket 1,p\rrbracket  :

\displaystyle E_{1}=\{2,2,4,5,7\} ; \displaystyle E_{2}=\{7,10,10,13\} et \displaystyle E_{3}=\{8,8,8\}.

 

La population P

• l’effectif total (N = 12)
• la somme des 12 observations \displaystyle\big(\sum_{i,k} x_{ik} {\;= 84}\big)
• la moyenne \displaystyle (\overline{\overline x } {\;= 7})

Les sous-populations \displaystyle (E_{k}\;\;k\in{1,2,3})

• les effectifs \displaystyle (n_{1}{\;= 5}) ; \displaystyle (n_{2}{\;= 4}); ; \displaystyle (n_{3}{\;= 3})
• les moyennes \displaystyle (\overline{x_1} {\;= 4}) ; \displaystyle (\overline{x_2} {\;= 10}) ; \displaystyle (\overline{x_3} {\;= 8}).

On retrouve la moyenne de la population : \displaystyle (\overline{\overline x } {\;=\frac{n_1\overline{x_1}+n_2\overline{x_2}+n_3\overline{x_3}}{N}}=7)

Rappelons d’une manière générale, le principe de calcul d’une variance :

1. évaluer, pour chaque valeur, l’écart à la moyenne : \displaystyle x_{i}-m,
2. élever au carré : \displaystyle (x_{i}-m)^2
3. faire la somme puis la moyenne : \displaystyle\frac{\sum_i(x_{i}-m)^2}{n}

On complète le tableau : \displaystyle (\overline{\overline x } {\;= 7})

	\displaystyle x_{ik}	\displaystyle (x_{ik}-\overline{x_k} )^2	\displaystyle</p> <p>(\overline{x_k}-\overline{\overline x } )^2	\displaystyle (x_{ik}-\overline{\overline x } )^2
\displaystyle\overline{x_1} {\;= 4}	2	4	9	25
	2	4	9	25
	4	0	9	9
	5	1	9	4
	7	9	9	0
\displaystyle\overline{x_2} {\;= 10}	7	9	9	0
	10	0	9	9
	10	0	9	9
	13	9	9	36
\displaystyle\overline{x_3} {\;= 8}	8	0	1	1
	8	0	1	1
	8	0	1	1
SOMME →	84	36	84	120
MOYENNE →	7	3	7	10

On distingue 3 variances :

variance_intra  = \displaystyle\frac{\sum_{i,k}(x_{ik}-\overline{x_k} )^2}{N}=3

variance_inter  = \displaystyle\frac{\sum_{k}n_k(\overline{x_k}-\overline{\overline x})^2}{N}=7

variance_totale  = \displaystyle\frac{\sum_{i,k}(x_{ik}-\overline{\overline x})^2}{N}=10

On constate sur cet exemple  :  variance_totale  = variance_intra  + variance_inter

Ce résultat se généralise. (cf. démonstration)