Considérons le test de comparaison d’une moyenne \displaystyle\mu à une valeur de référence \displaystyle\mu_0
H0 : \displaystyle\mu{\;=\;\mu_0} opposée à H1 : \displaystyle\mu{\; \neq\;\mu_0}
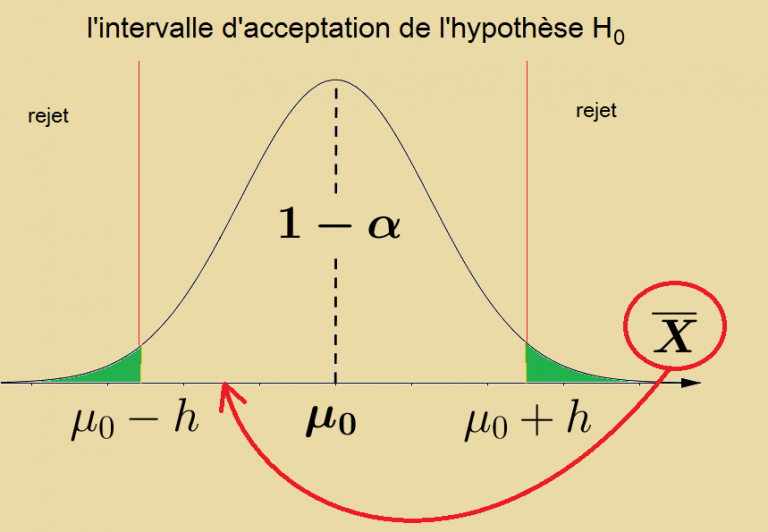
l’intervalle d’acceptation de l’hypothèse nulle H0
A partir
- de la loi d’échantillonnage : la loi suivie par la moyenne \displaystyle \overline X de l’échantillon de taille n,
- du risque α
on établit l’intervalle d’acceptation de H0 en recherchant le réel h tel que :
| \displaystyle P\;(\overline{X} \in\big[\mu_0-h\;;\;\mu_0+h\big]){= 1-\alpha} |
En pratique, le rejet répété de l’hypothèse H0 (supposée vraie), conduit à douter de la valeur de référence μ0 et à proposer une autre valeur μ1 :
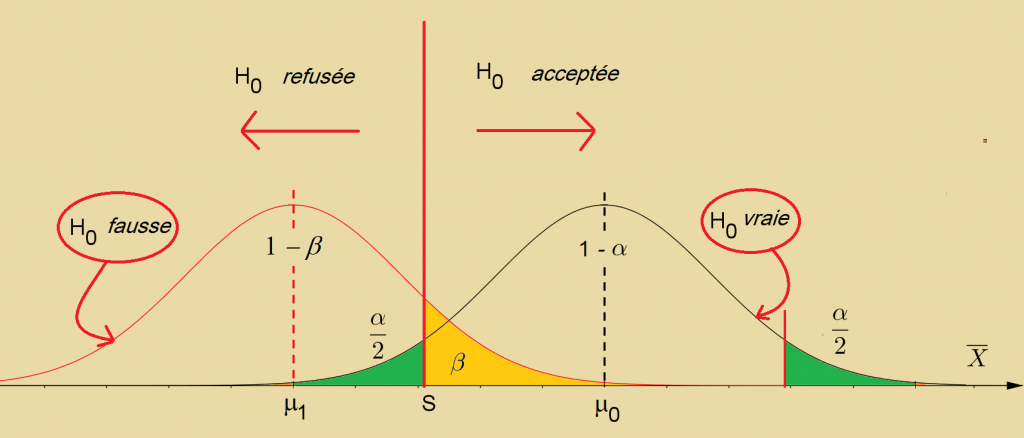
Le refus de H0 à bon escient est la puissance du test, de probabilité 1-β.
Les risques α et β fixés
- La loi d’échantillonnage se présente selon l’hypothèse H0 :
| H0 vraie | H0 fausse |
| \displaystyle \overline{X}\hookrightarrow\mathcal{N}(\mu_0\;;\;\frac{\sigma}{\sqrt{n}}) | \displaystyle \overline{X}\hookrightarrow\mathcal{N}(\mu_1\;;\;\frac{\sigma}{\sqrt{n}}) |
- En désignant par S le seuil à partir duquel on accepte l’hypothèse H0 , les risques α et β se définissent ainsi :
| H0 vraie | H0 fausse |
| \displaystyle \frac{\alpha}{2}=P(\overline{X}\le S) | \displaystyle\beta=P(\overline{X}\ge S) |
| (en désignant par T la variable de loi normale centrée réduite) | |
| \displaystyle \frac{\alpha}{2}=P(T\le -t_0)
Exemple : α = 5% t0 = 1,96 |
\displaystyle \beta=P(T\ge t_1)
Exemple : β = 10% t1 = 1,28 |
donc, simultanément on a :
\displaystyle \frac{S-\mu_0}{\sigma}\times\sqrt{n}=-t_0 et \displaystyle \frac{S-\mu_1}{\sigma}\times\sqrt{n}=t_1
\displaystyle S=\mu_0-t_0\times\frac{\sigma}{\sqrt{n}} et \displaystyle S=\mu_1+t_1\times\frac{\sigma}{\sqrt{n}}
d’où, la relation : (en éliminant S des 2 équations)
\displaystyle (\mu_0-\mu_1)\times\sqrt{n}=(t_0+t_1)\times\sigma
et ainsi, en désignant par Δ l’écart entre les 2 valeurs de référence proposées :
| \displaystyle \Delta\times\sqrt{n}=(t_0+t_1)\times\sigma |
l’écart Δ entre les 2 valeurs de référence
| \displaystyle \Delta=\frac{(t_0+t_1)\times\sigma}{\sqrt{n}} |
le nombre n de mesures à effectuer
| \displaystyle n=\Big(\frac{(t_0+t_1)\times\sigma}{\Delta}\Big)^2 |