Soit une population P \displaystyle \Big\{\begin{array}l{\mu} \\{\sigma=5}\end{array}
où μ la moyenne est inconnue, σ l’écart type est égal à 5.
les hypothèses
- une hypothèse préférentielle (supposée vraie) H0 : \displaystyle\mu{\;= 12}
- une hypothèse rivale H1 : \displaystyle\mu{\; \neq 12}
Marche à suivre
H0 vraie —> Test —-> Décision \displaystyle \Big\{\begin{array}l{acceptation} \\{rejet}\end{array} (risque α)
décider à partir de la moyenne d’un échantillon de taille n=4
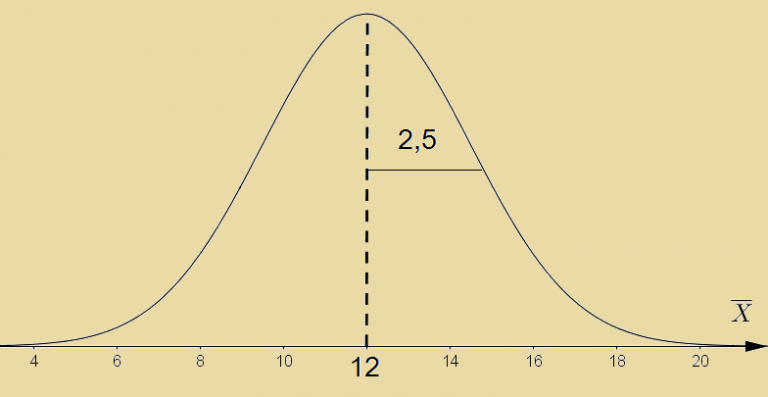
La loi de probabilité suivie par la moyenne \displaystyle \overline X de l’échantillon de taille n, est la loi normale. Plus précisément :
| \displaystyle \overline{X} suit loi normale de moyenne μ et d’écart type \displaystyle \frac{\sigma}{\sqrt{n}} (appelée : la loi d’échantillonnage) |
Donc, dans le contexte : H0 est vraie, σ=5 et n=4.
| \displaystyle \overline{X} \hookrightarrow\mathcal{N}(12\;;\;{2,5}) |
Dans la prise de décision, il faut accepter de prendre un risque : celui de pouvoir se tromper.
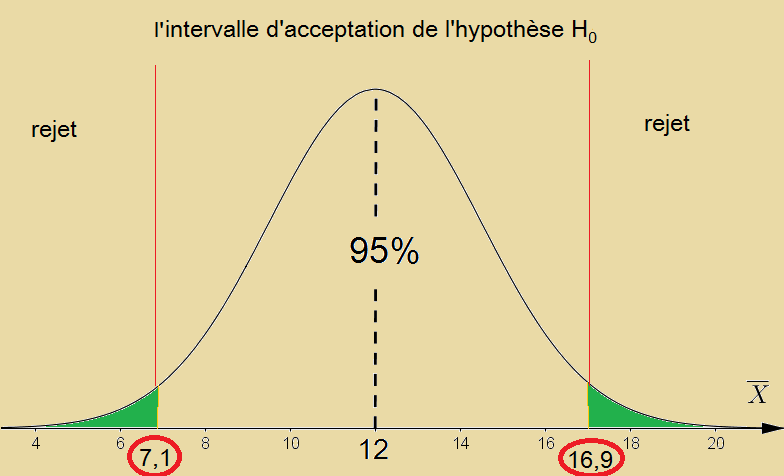
On convient d’un risque α à hauteur de 5% et on contrôle, à l’aide d’un logiciel ou d’un calcul, l’intervalle d’acceptation de H0 :
| \displaystyle P\;(\overline{X} \in\big[7,1\;;\;16,9\big]){= 0,95} |
le test ou règle de décision
On observe sur un échantillon de 4 individus de la population P une moyenne \displaystyle \overline x.
- si \displaystyle \overline x\in\big[7,1\;;\;16,9\big] alors l’hypothèse H0 est acceptée (*) ;
- si \displaystyle \overline x\notin\big[7,1\;;\;16,9\big] alors l’hypothèse H0 est refusée au risque α = 5%. (**)
(*) « il n’y a aucune raison de refuser H0 » .
On évite de mentionner le risque dans ce cas.
L’hypothèse H0 fausse et donc l’acceptation à tort ne sont pas envisagés. (risque β de seconde espèce)
(**) « il y a un risque de se tromper en refusant H0 » . Sous l’hypothèse H0 (vraie), on se trompe dans 5% des cas. (rejets à tort)
application : carte de contrôle de la moyenne
Dans l’industrie chimique, on contrôle la qualité de la production en continu à partir d’un prélèvement. Il faut « échantillonner » .
———– par exemple ——
Des échantillons de 4 mesures sont effectués toutes les heures dont l’objectif principal est de s’assurer du bon réglage du procédé.
12 est la valeur de consigne de réglage et la moyenne de l’échantillon permet de vérifier qu’il n’y a pas de variation significative.
On définit les limites de surveillance à 95%. (σ = 5). Les moyennes observées sur les échantillons sont des points placés sur la carte de contrôle en respectant l’ordre chronologique.
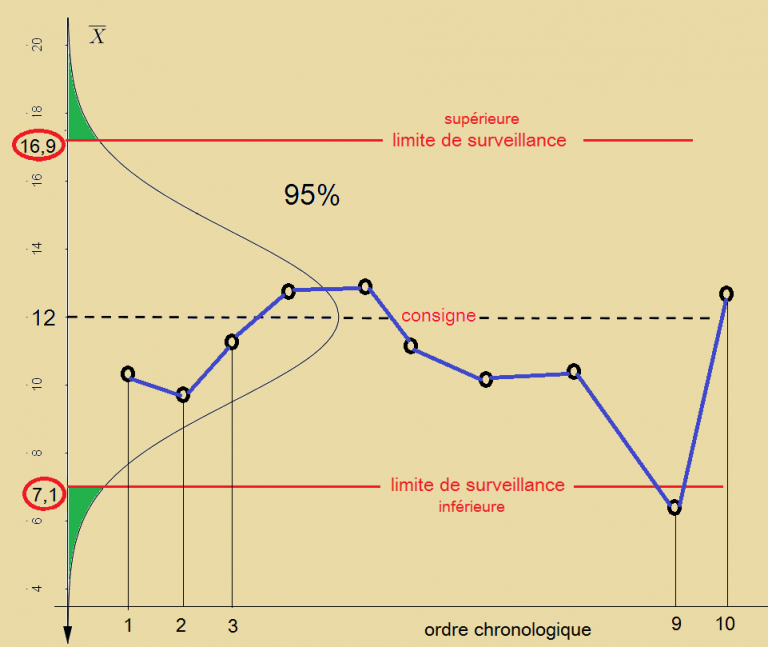
Tant que la vraie moyenne reste égale à 12 (hypothèse préférentielle H0 : μ = 12), on doit observer 95% des points entre les 2 limites de surveillance.
L’échantillon N°9 correspond à un dépassement du seuil de surveillance : soit une valeur assez peu probable (fausse alarme : 5% des points) soit un déréglage.